$\Delta_1$ is an equilateral triangle with unit length and we have a function $ f(x) $ which is used to create other triangles.

We create further triangles with the following rules:

We take $ \Delta_n $’s side and produce its sides clockwise till its new length is $ f(n) $ times the original length, and the final endpoints are joined to make $ \Delta_{n+1} $.

For example, if $ f(x) = 2 $:

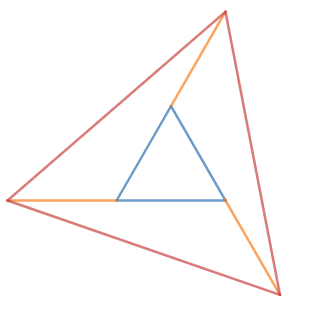
Here, if the Blue triangle is $ \Delta_n $, then the Red triangle is $ \Delta_{n+1} $, and the ratio of lengths $\frac{\text{Blue} + \text{Orange}}{\text{Blue}} = f(n)$, and the triangle rotates by $0.3334$ radians.

If $f(n) = \frac{2\sqrt{3}n^2-1}{2\sqrt{3}n^2-3}$, find the total rotation of $ \Delta_n $ in radians when compared to $ \Delta_1 $ as $ n \to \infty $.